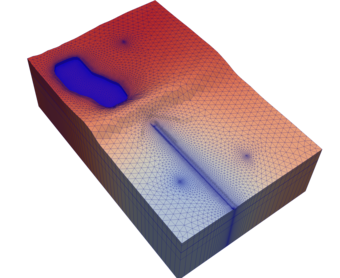
68 class(MethodSubcellTernaryType),
intent(inout) :: this
69 class(SubcellTriType),
intent(in) :: subcell
70 type(ParticleType),
pointer,
intent(inout) :: particle
71 real(DP),
intent(in) :: tmax
73 integer(I4B) :: exitFace
123 integer(I4B) :: izstatus
124 integer(I4B) :: itopbotexit
125 integer(I4B) :: ntmax
126 integer(I4B) :: isolv
127 integer(I4B) :: itrifaceenter
128 integer(I4B) :: itrifaceexit
133 integer(I4B) :: reason
137 if (particle%iexmeth == 0)
then
140 isolv = particle%iexmeth
166 vzbot = subcell%vzbot
167 vztop = subcell%vztop
179 call canonical(x0, y0, x1, y1, x2, y2, &
180 v0x, v0y, v1x, v1y, v2x, v2y, &
182 rxx, rxy, ryx, ryy, &
184 alp0, bet0, alp1, bet1, alp2, bet2, alpi, beti)
188 call clamp_bary(alpi, beti, gami, pad=dsame * dep3)
193 zirel = (zi - zbot) / dz
194 if (zirel > done)
then
199 call calculate_dt(vzbot, vztop, dz, zirel, vzi, &
200 az, dtexitz, izstatus, &
205 itrifaceenter = particle%iboundary(3) - 1
206 if (itrifaceenter == -1) itrifaceenter = 999
207 call traverse_triangle(isolv, tol, &
208 dtexitxy, alpexit, betexit, &
209 itrifaceenter, itrifaceexit, &
210 alp1, bet1, alp2, bet2, alpi, beti)
214 if (itopbotexit == 0 .and. itrifaceexit == 0)
then
216 particle%advancing = .false.
217 call this%save(particle, reason=3)
225 if (itrifaceexit /= 0)
then
227 exitface = itrifaceexit
229 else if (dtexitz < dtexitxy .and. dtexitz >= 0.0_dp)
then
231 if (itopbotexit == -1)
then
239 particle%advancing = .false.
240 call this%save(particle, reason=3)
243 texit = particle%ttrack + dtexit
250 call this%tracktimes%advance()
251 if (this%tracktimes%any())
then
252 do i = this%tracktimes%selection(1), this%tracktimes%selection(2)
253 t = this%tracktimes%times(i)
254 if (t < particle%ttrack) cycle
255 if (t >= texit .or. t >= tmax)
exit
257 call calculate_xyz_position(dt, rxx, rxy, ryx, ryy, sxx, sxy, syy, &
258 izstatus, x0, y0, az, vzi, vzbot, &
259 ztop, zbot, zi, x, y, z)
265 call this%save(particle, reason=5)
272 if (texit .gt. tmax)
then
279 particle%advancing = .false.
288 call calculate_xyz_position(dt, rxx, rxy, ryx, ryy, sxx, sxy, syy, &
289 izstatus, x0, y0, az, vzi, vzbot, &
290 ztop, zbot, zi, x, y, z, exitface)
295 particle%iboundary(3) = exitface
297 call this%save(particle, reason=reason)
@ term_no_exits_sub
terminated in a subcell with no exit face