mathutilmodule Module Reference

Data Types
interface	mod_offset
interface	f1d

Functions/Subroutines
pure logical function, public	is_close (a, b, rtol, atol, symmetric)
	Check if a real value is approximately equal to another. More...
pure integer(i4b) function	mod_offset_int (a, n, d)
	Modulo with offset for integer values. More...
pure real(dp) function	mod_offset_dbl (a, n, d)
	Modulo with offset for double precision values. More...
real(dp) function, public	zero_ch (x0, x1, f, epsa)
	Compute zeros on an interval using Chadrupatla's method. More...
real(dp) function, public	zero_br (ax, bx, f, tol)
	Compute a zero of the function f(x) in the interval (x0, x1). More...
real(dp) function, public	get_perturbation (x)
	Calculate a numerical perturbation given the value of x. More...
pure real(dp) function, dimension(:), allocatable, public	arange (start, stop, step)
	Return reals separated by the given step over the given interval. More...
pure real(dp) function, dimension(:), allocatable, public	linspace (start, stop, num)
	Return evenly spaced reals over the given interval. More...

Function/Subroutine Documentation

arange()

pure real(dp) function, dimension(:), allocatable, public mathutilmodule::arange	(	real(dp), intent(in)	start,
		real(dp), intent(in)	stop,
		real(dp), intent(in), optional	step
	)

This function is designed to behave like NumPy's arange. Adapted from https://stackoverflow.com/a/65839162/6514033.

Definition at line 383 of file MathUtil.f90.

    ! dummy
    real(DP), intent(in) :: start, stop
    real(DP), intent(in), optional :: step
    real(DP), allocatable :: array(:)
    ! local
    real(DP) :: lstep
    integer(I4B) :: i, n
 
    if (present(step)) then
      lstep = step
    else
      lstep = done
    end if
 
    if (step <= 0) then
      allocate (array(0))
    else
      n = ceiling((stop - start) / step)
      allocate (array(n))
      do i = 0, n - 1
        array(i + 1) = start + step * i
      end do
    end if

Here is the caller graph for this function:

get_perturbation()

real(dp) function, public mathutilmodule::get_perturbation

(

real(dp), intent(in)

x

)

Calculate a perturbation value to use for a numerical derivative calculation. Taken from the book "Solving Nonlinear Equations with Newton's Method" 2003, by C.T. Kelley. Method also used in the SWR Process for MODFLOW-2005.

Parameters

[in]

x

value that will be perturbed by the result

Returns

calculated perturbation value

Definition at line 371 of file MathUtil.f90.

    use constantsmodule, only: dprecsqrt, done
    real(DP), intent(in) :: x !< value that will be perturbed by the result
    real(DP) :: res !< calculated perturbation value
    res = dprecsqrt * max(abs(x), done) * sign(done, x)

Here is the caller graph for this function:

is_close()

pure logical function, public mathutilmodule::is_close	(	real(dp), intent(in)	a,
		real(dp), intent(in)	b,
		real(dp), intent(in), optional	rtol,
		real(dp), intent(in), optional	atol,
		logical(lgp), intent(in), optional	symmetric
	)

By default the determination is symmetric in a and b, as in Python's math.isclose, with relative difference scaled by a factor of the larger absolute value of a and b. The formula is: abs(a - b) <= max(rtol * max(abs(a), abs(b)), atol).

If symmetric is set to false the test is asymmetric in a and b, with b taken to be the reference value, and the alternate formula (abs(a - b) <= (atol + rtol * abs(b))) is used. This is the approach taken by numpy.allclose.

Defaults for rtol and atol are DSAME and DZERO, respectively. If a or b are near 0 (especially if either is 0), an absolute tolerance suitable for the particular case should be provided. For a justification of a zero absolute tolerance default see: https://peps.python.org/pep-0485/#absolute-tolerance-default

Parameters

[in]	a	first real
[in]	b	second real (reference value if asymmetric)
[in]	rtol	relative tolerance (default=DSAME)
[in]	atol	absolute tolerance (default=DZERO)
[in]	symmetric	toggle (a)symmetric comparison

Definition at line 45 of file MathUtil.f90.

    ! dummy
    real(DP), intent(in) :: a !< first real
    real(DP), intent(in) :: b !< second real (reference value if asymmetric)
    real(DP), intent(in), optional :: rtol !< relative tolerance (default=DSAME)
    real(DP), intent(in), optional :: atol !< absolute tolerance (default=DZERO)
    logical(LGP), intent(in), optional :: symmetric !< toggle (a)symmetric comparison
    ! local
    real(DP) :: lrtol, latol
    logical(LGP) :: lsymmetric
 
    ! check for exact equality
    if (a == b) then
      is_close = .true.
      return
    end if
 
    ! process optional arguments
    if (.not. present(rtol)) then
      lrtol = dsame
    else
      lrtol = rtol
    end if
    if (.not. present(atol)) then
      latol = dzero
    else
      latol = atol
    end if
    if (.not. present(symmetric)) then
      lsymmetric = .true.
    else
      lsymmetric = symmetric
    end if
 
    if (lsymmetric) then
      ! "weak" symmetric test, https://peps.python.org/pep-0485/#which-symmetric-test
      is_close = abs(a - b) <= max(lrtol * max(abs(a), abs(b)), latol)
    else
      ! asymmetric, https://numpy.org/doc/stable/reference/generated/numpy.isclose.html
      is_close = (abs(a - b) <= (latol + lrtol * abs(b)))
    end if

Here is the caller graph for this function:

linspace()

pure real(dp) function, dimension(:), allocatable, public mathutilmodule::linspace	(	real(dp), intent(in)	start,
		real(dp), intent(in)	stop,
		integer(i4b), intent(in)	num
	)

This function is designed to behave like NumPy's linspace. Adapted from https://stackoverflow.com/a/57211848/6514033.

Definition at line 414 of file MathUtil.f90.

    ! dummy
    real(DP), intent(in) :: start, stop
    integer(I4B), intent(in) :: num
    real(DP), allocatable :: array(:)
    ! local
    real(DP) :: range
    integer(I4B) :: i
 
    allocate (array(num))
    range = stop - start
 
    if (num == 0) return
    if (num == 1) then
      array(1) = start
      return
    end if
    do i = 1, num
      array(i) = start + range * (i - 1) / (num - 1)
    end do

mod_offset_dbl()

pure real(dp) function mathutilmodule::mod_offset_dbl ( real(dp), intent(in)  a, real(dp), intent(in)  n, real(dp), intent(in), optional  d  )

private

Parameters

[in]	a	dividend
[in]	n	divisor
[in]	d	offset

Definition at line 107 of file MathUtil.f90.

    ! -- dummy
    real(DP), intent(in) :: a !< dividend
    real(DP), intent(in) :: n !< divisor
    real(DP), intent(in), optional :: d !< offset
    real(DP) :: mo
    ! -- local
    real(DP) :: ld
 
    if (present(d)) then
      ld = d
    else
      ld = 0
    end if
    mo = a - n * floor((a - ld) / n)

mod_offset_int()

pure integer(i4b) function mathutilmodule::mod_offset_int ( integer(i4b), intent(in)  a, integer(i4b), intent(in)  n, integer(i4b), intent(in), optional  d  )

private

Parameters

[in]	a	dividend
[in]	n	divisor
[in]	d	offset

Definition at line 89 of file MathUtil.f90.

    ! -- dummy
    integer(I4B), intent(in) :: a !< dividend
    integer(I4B), intent(in) :: n !< divisor
    integer(I4B), intent(in), optional :: d !< offset
    integer(I4B) :: mo
    ! -- local
    integer(I4B) :: ld
 
    if (present(d)) then
      ld = d
    else
      ld = 0
    end if
    mo = a - n * floor(real(a - ld) / n)

zero_br()

real(dp) function, public mathutilmodule::zero_br	(	real(dp)	ax,
		real(dp)	bx,
		procedure(f1d), intent(in), pointer	f,
		real(dp)	tol
	)

A zero of the function f(x) is computed in the interval ax,bx.

Input:

ax left endpoint of initial interval bx right endpoint of initial interval f function subprogram which evaluates f(x) for any x in the interval ax,bx tol desired length of the interval of uncertainty of the final result (.ge.0.)

Output:

zero_br abscissa approximating a zero of f in the interval ax,bx

it is assumed  that   f(ax)   and   f(bx)   have  opposite  signs

this is checked, and an error message is printed if this is not satisfied. zero_br returns a zero x in the given interval ax,bx to within a tolerance 4*macheps*abs(x)+tol, where macheps is the relative machine precision defined as the smallest representable number such that 1.+macheps .gt. 1. this function subprogram is a slightly modified translation of the algol 60 procedure zero given in richard brent, algorithms for minimization without derivatives, prentice-hall, inc. (1973).

This subroutine was obtained by the authors of MODFLOW 6 from netlib.org with the understanding that it is freely available. It has subsequently undergone minor modification to suit the current application.

Definition at line 254 of file MathUtil.f90.

    ! -- dummy
    real(DP) :: ax, bx
    procedure(f1d), pointer, intent(in) :: f
    real(DP) :: tol
    real(DP) :: z
    ! -- local
    real(DP) :: eps
    real(DP) :: a, b, c, d, e, s, p, q
    real(DP) :: fa, fb, fc, r, tol1, xm
    logical(LGP) :: rs
 
    eps = epsilon(ax)
    tol1 = eps + done
 
    a = ax
    b = bx
    fa = f(a)
    fb = f(b)
 
    ! check if a or b is the solution
    if (fa == dzero) then
      z = a
      return
    else if (fb == dzero) then
      z = b
      return
    end if
 
    ! check that f(ax) and f(bx) have opposite sign
    if (fa * (fb / dabs(fb)) .ge. dzero) &
      call pstop(1, 'f(ax) and f(bx) do not have different signs,')
 
    rs = .true. ! var reset
    do while (.true.)
      if (rs) then
        c = a
        fc = fa
        d = b - a
        e = d
      end if
 
      if (.not. (dabs(fc) .ge. dabs(fb))) then
        a = b
        b = c
        c = a
        fa = fb
        fb = fc
        fc = fa
      end if
 
      tol1 = dtwo * eps * dabs(b) + dhalf * tol
      xm = dhalf * (c - b)
      if ((dabs(xm) .le. tol1) .or. (fb .eq. dzero)) then
        z = b
        return
      end if
 
      ! see if a bisection is forced
      if ((dabs(e) .ge. tol1) .and. (dabs(fa) .gt. dabs(fb))) then
        s = fb / fa
        if (a .ne. c) then
          ! inverse quadratic interpolation
          q = fa / fc
          r = fb / fc
          p = s * (dtwo * xm * q * (q - r) - (b - a) * (r - done))
          q = (q - done) * (r - done) * (s - done)
        else
          ! linear interpolation
          p = dtwo * xm * s
          q = done - s
        end if
 
        if (p .le. dzero) then
          p = -p
        else
          q = -q
        end if
        s = e
        e = d
        if (((dtwo * p) .ge. (dthree * xm * q - dabs(tol1 * q))) .or. &
            (p .ge. dabs(dhalf * s * q))) then
          d = xm
          e = d
        else
          d = p / q
        end if
      else
        d = xm
        e = d
      end if
 
      a = b
      fa = fb
 
      if (dabs(d) .le. tol1) then
        if (xm .le. dzero) then
          b = b - tol1
        else
          b = b + tol1
        end if
      else
        b = b + d
      end if
 
      fb = f(b)
      rs = (fb * (fc / dabs(fc))) .gt. dzero
    end do

Here is the call graph for this function:

Here is the caller graph for this function:

zero_ch()

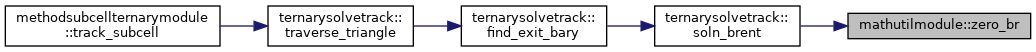
real(dp) function, public mathutilmodule::zero_ch	(	real(dp)	x0,
		real(dp)	x1,
		procedure(f1d), intent(in), pointer	f,
		real(dp)	epsa
	)

A zero of the function f{x} is computed in the interval (x0, x1) given tolerance epsa using Chandrupatla's method. FORTRAN code based generally on pseudocode in Scherer, POJ (2013) "Computational Physics: Simulation of Classical and Quantum Systems," 2nd ed., Springer, New York.

Definition at line 131 of file MathUtil.f90.

    ! -- dummy
    real(DP) :: x0, x1
    procedure(f1d), pointer, intent(in) :: f
    real(DP) :: epsa
    real(DP) :: z
    ! -- local
    real(DP) :: epsm
    real(DP) :: a, b, c, t
    real(DP) :: aminusb, cminusb
    real(DP) :: fa, fb, fc, fm, ft
    real(DP) :: faminusfb, fcminusfb
    real(DP) :: phi, philo, phihi
    real(DP) :: racb, rcab, rbca
    real(DP) :: tol, tl, tlc
    real(DP) :: xi, xm, xt
 
    epsm = epsilon(x0)
    b = x0
    a = x1
    c = x1
    aminusb = a - b
    fb = f(b)
    fa = f(a)
    fc = f(c)
    t = 5d-1
 
    ! check whether a or b is the solution
    if (fa == dzero) then
      z = a
      return
    else if (fb == dzero) then
      z = b
      return
    end if
 
    do while (.true.)
      xt = a - t * aminusb
      ft = f(xt)
      if (sign(ft, fa) == ft) then
        c = a
        fc = fa
        a = xt
        fa = ft
      else
        c = b
        b = a
        a = xt
        fc = fb
        fb = fa
        fa = ft
      end if
      aminusb = a - b
      cminusb = c - b
      faminusfb = fa - fb
      fcminusfb = fc - fb
      xm = a
      fm = fa
      if (dabs(fb) < dabs(fa)) then
        xm = b
        fm = fb
      end if
      tol = dtwo * epsm * dabs(xm) + epsa
      tl = tol / dabs(cminusb)
      if ((tl > 5d-1) .or. (fm == dzero)) then
        z = xm
        return
      end if
      xi = aminusb / cminusb
      phi = faminusfb / fcminusfb
      philo = done - dsqrt(done - xi)
      phihi = dsqrt(xi)
      if ((phi > philo) .and. (phi < phihi)) then
        racb = fa / fcminusfb
        rcab = fc / faminusfb
        rbca = fb / (fc - fa)
        t = racb * (rcab - rbca * (c - a) / aminusb)
        if (t < tl) then
          t = tl
        else
          tlc = done - tl
          if (t > tlc) then
            t = tlc
          end if
        end if
      else
        t = 5d-1
      end if
    end do

Here is the caller graph for this function: